learnDataStructures

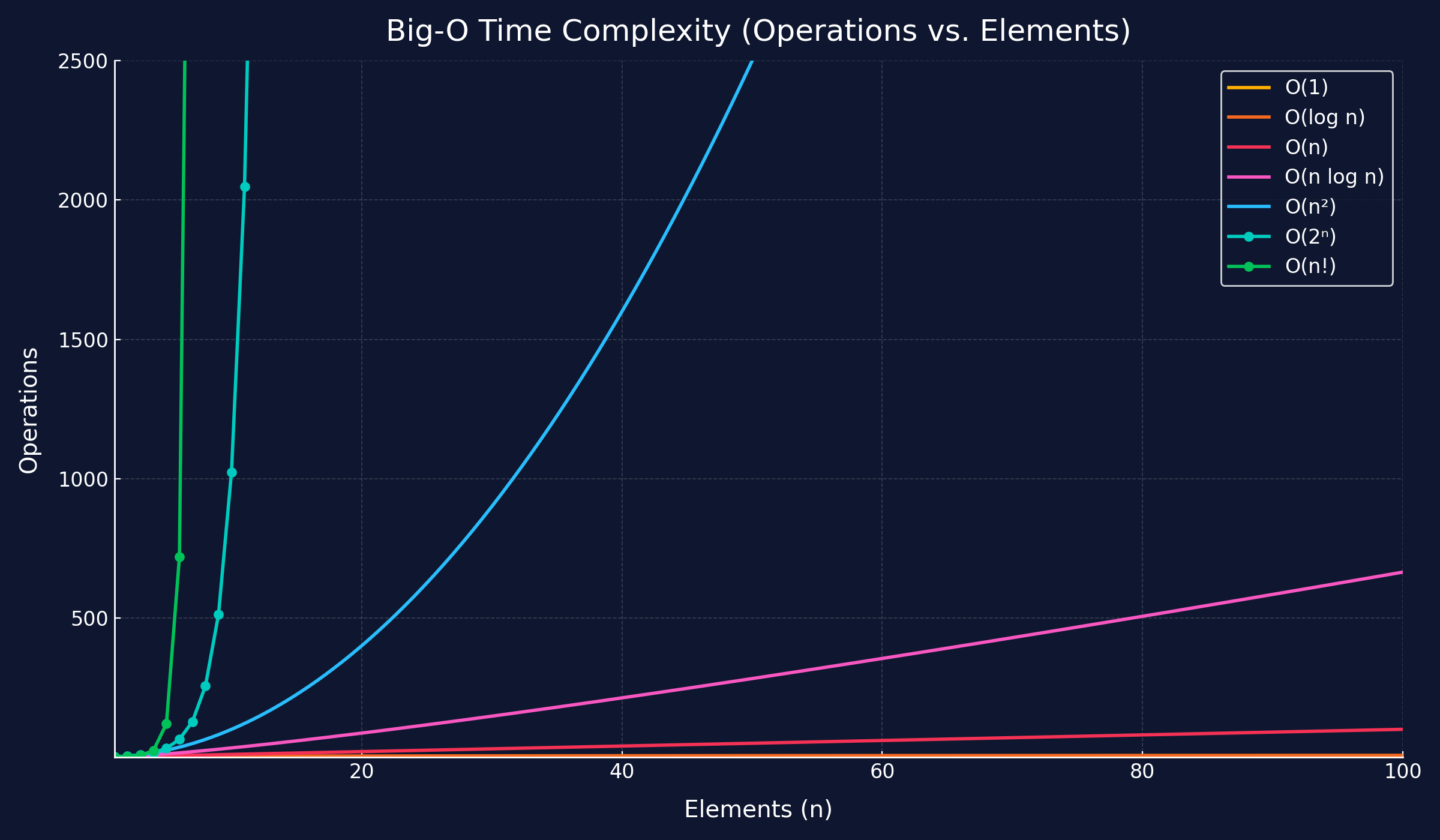
Time complexity describes how an algorithm’s running time grows as the input size n increases. It’s hardware-independent and counts elementary operations (comparisons, moves, arithmetic, etc.).

• Big-O upper bound: worst-case growth (e.g., quicksort is O(n²) worst-case).
• Big-Ω lower bound: best-case growth (e.g., linear search is Ω(1) if the key is first).
• Big-Θ tight bound: same order above and below (e.g., mergesort is Θ(n log n)).

Note: Time Complexity measures growth with respect to input size, not the execution time.

Scaling equations

• Predict time for a new size: t₂ = t₁ × f(n₂)/f(n₁)
• Predict size for a time budget: find n₂ with f(n₂) = (t₂/t₁) · f(n₁)

Powers: f(n)=n^k ⇒ n₂ = n₁ · (t₂/t₁)^{1/k}. Logs: f(n)=\log n ⇒ n₂ = n₁^{(t₂/t₁)}. For n\log n, solve numerically (the calculator below does that).

Counting rules

• Ignore constants and lower-order terms: 7n + 3 → O(n), n + n log n → O(n log n).
• Sequential parts add (dominated by the largest order). Nested loops multiply.
• Recurrences capture divide-and-conquer time.

Recurrence cheat-sheet

Recurrence	Solution	Appears in
T(n)=T(n/2)+c	Θ(\log n)	Binary search
T(n)=2T(n/2)+cn	Θ(n\log n)	Mergesort, FFT
T(n)=T(n-1)+c	Θ(n)	Linear recursion
T(n)=T(n-1)+n	Θ(n^2)	Triangular loops / insertion sort worst

Examples

Example 1 — Quadratic scaling
t₁ = 200 ms for n₁ = 1000, algorithm O(n²).
t₂ = t₁ × (n₂² / n₁²).
If n₂ = 3000 → t₂ = 200 × (3000/1000)² = 200 × 9 = 1800 ms.

Example 2 — Logarithmic scaling
t₁ = 200 ms for n₁ = 1000, algorithm O(log n).
t₂ = t₁ × (log n₂ / log n₁).
If t₂ = 1800 ms:
  1800/200 = 9 = log n₂ / log 1000 ⇒ log n₂ = 27 ⇒ n₂ = 10²⁷.

Common classes & examples

Notation	Name	Typical examples
O(1)	Constant	Hash lookup (avg), stack push/pop
O(log n)	Logarithmic	Binary search; balanced BST height
O(n)	Linear	Single pass, two-pointer scan
O(n log n)	Log-linear	Mergesort/Heapsort; many divide-and-conquer
O(n^2)	Quadratic	Double loop; selection/bubble sort
O(2^n)	Exponential	Enumerate all subsets
O(n!)	Factorial	All permutations; naive TSP

A) Time scaling: t₂ from n₂

B) Throughput scaling: n₂ from t₂

Both calculators assume the same constant factor/hardware between scenarios.